LCS とは
LCS: Longest Common Subsequence(最長共通部分列) 問題とは、2 つのシーケンスから最長の共通部分列を探す問題です。
部分列は飛び飛びの要素で構成されていても構いませんが、順番はキープして作成する必要があります。下記の例は、2 つの文字列とその最長共通部分列 (LCS) を示したものです。
- 文字列1: "ABCDCE"
- 文字列2: "ACCDEX"
- LCS: "ACCE" or "ACDE"
LCS の計算方法
LCS は、動的計画法(DP: Dynamic Programming)の例題としてよく示される問題で、DP を使うことで効率的に答えを求めることができます。 考え方としては、下記のような文字列の入ったスタックから、任意の順番で文字を取り出していく問題だとみなすと分かりやすいです。
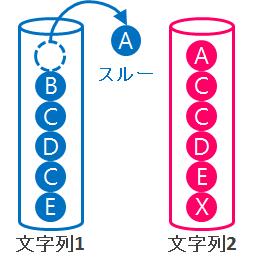
どちらか一方から要素を取り出すときは、文字をマッチさせないと考えます。 両方の要素を同時に取り出すときは、そのタイミングで文字をマッチさせる(LCS を構成する要素)と考えます。
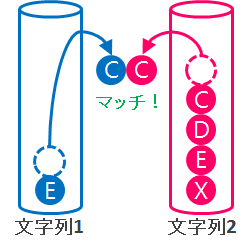
このように、任意の順番で取り出してマッチングしていったときに、最大の一致数になったものが LCS ということになります。
ここでは、DP(動的計画法)を使って、文字列 1 と文字列 2 の LCS の長さを求めるコードを考えてみます。
- 文字列 1 の長さを
Len1、文字列 2 の長さをLen2とします。 dp[i][j]には、文字列 1 のj文字目までの部分文字列と、文字列 2 のi文字目までの部分文字列を一致させた場合 LCS の長さを格納します。
まず、0 文字の部分文字列同士の LCS は当然 0 文字なので、
dp[0][0] = 0となります。
dp[0][i] は、文字列 1 の i 文字目までの部分文字列と、空文字列(文字列 2 の 0 文字目まで)の LCS の長さを示しています。
一方が空文字なので、結局 LCS の長さは 0 です。
同様に、dp[i][0] もすべて 0 です。
dp 配列をテーブルで示すと下記のようになります。
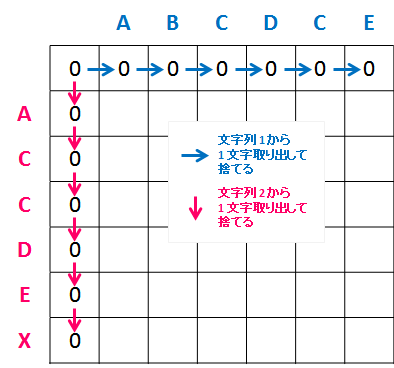
右方向に移動していくのは文字列 1 ("ABCDCE") から一文字を取り出して捨てること、下方向に移動していくのは文字列 2 ("ACCDEX") から一文字を取り出して捨てることを示しています。 その文字を LCS の候補とみなさずに捨てるだけなので、最大長は変化しません。
取り出そうとしている文字が一致する場合は、LCS の候補としてマッチさせることができます。 このテーブル上では、斜め方向に移動することで表現します。
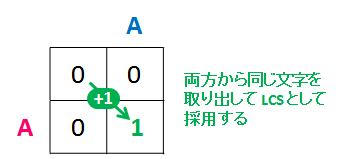
この斜め移動は、それぞれの文字列から同じ文字を取り出して LCS の文字として採用することを表すので、最大長 +1 ということになります。
dp[1][1] = dp[0][0] + 12 つの文字列から 1 文字ずつ取り出す方法は、このように LCS の候補としてマッチさせる方法と、それぞれの文字を LCS の候補とみなさずに捨てる方法(下図)があります。
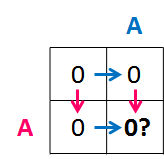
文字を捨てるだけの場合は、LCS 最大長は変化しないので dp[1][1] = 0 のままです。
dp[i][j] には、i 文字、j 文字を消費するパターンのうち、LCS 長が最大になる値を格納すればよいので、結果として dp[1][1] は 1 と求まります。
ここまでの処理は下記のような漸化式として表現できます。
dp[i][j] は下記の最大値:
* dp[i][j-1] #左から進んでくるケース(文字列 1 から一文字削除)
* dp[i-1][j] #上から進んでくるケース(文字列 2 から一文字削除)
* dp[i-1][j-1] + 1 #LCS の候補とみなした場合(同じ文字の場合のみ)i, j の小さい順に求めていくと、dp 配列全体の値が求まり、最終的に以下のようになります。
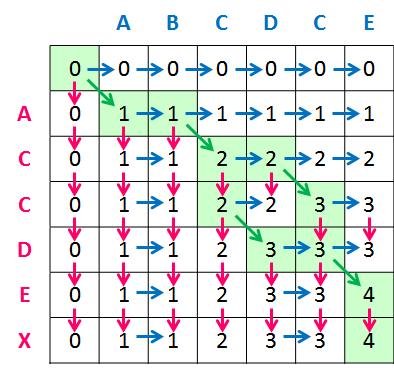
右下の値 (4) が LCS 最大長を表しています。 斜めに進んでいる部分が、文字をマッチさせたタイミングを表していて、LCS の候補として "ACCE" と "ACDE" の二通りがあることが分かります。
Java による LCS の実装例
下記は Java で LCS を求めるサンプルコードです。
public class LcsSample {
/**
* Calculate the length of the LCS (Longest Common Sequence).
*
* @param s1 the first string to be compared, not null
* @param s2 the second string to be compared, not null
* @return the length of the LCS
* @see http://en.wikipedia.org/wiki/Longest_common_subsequence_problem
*/
public static int lcs(String s1, String s2) {
int len1 = s1.length();
int len2 = s2.length();
// 配列初期値は 0 なので dp 配列の初期化は不要
int dp[][] = new int[len2 + 1][len1 + 1];
for (int i = 1; i <= len2; ++i) {
for (int j = 1; j <= len1; ++j) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
if (s1.charAt(j - 1) == s2.charAt(i - 1)) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] + 1);
}
}
}
return dp[len2][len1];
}
public static void main(String[] args) {
System.out.println(lcs("", "A")); // 0
System.out.println(lcs("AC", "AB")); // 1 "A"
System.out.println(lcs("ABC", "ACB")); // 2 "AB or "AC"
System.out.println(lcs("AGCAT", "GAC")); // 2
System.out.println(lcs("ABCDCE", "ACCDEX")); // 4 "ACCE" or "ACDE"
}
}実は、dp[i][j] を更新する部分は、次のように最適化することができます。
if (s1.charAt(j - 1) == s2.charAt(i - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}斜めに移動できるケースの場合は、必ず斜めに移動させた方が LCS の最大長を +1 できて有利だからです。
さらに、一行ずつ dp 配列を求めていることを考えると、実は二次元配列ではなく、一次元配列を使って計算することもできます。
private static int lcs(String s1, String s2) {
int len1 = s1.length();
int len2 = s2.length();
int[] dp1 = new int[len1 + 1];
int[] dp2 = new int[len1 + 1];
for (int i = 1; i <= len2; ++i) {
for (int j = 1; j <= len1; ++j) {
if (s1.charAt(j - 1) == s2.charAt(i - 1)) {
dp2[j] = dp1[j - 1] + 1;
} else {
dp2[j] = Math.max(dp2[j - 1], dp1[j]);
}
}
// Swap buffers
int[] temp = dp1;
dp1 = dp2;
dp2 = temp;
}
return dp1[len1];
}