まくろぐ
更新: / 作成:

レーベンシュタイン距離とは

レーベンシュタイン距離 (Levenshtein Distance) は、ある文字列に対して、何回の変更処理（削除、挿入、置換）を行えば対象の文字列に変換できるかを示します。

レーベンシュタイン距離を効率的に計算するために、一般的に DP マッチング（動的計画法による距離計算）が使用されます（ここでは文字列間の距離を求めていますが、DP マッチングは単純に二つの波形を伸縮させながらマッチングするためにも使用されます）。 下記に詳細なマッチングの過程を示します。

2 つの文字列のレーベンシュタイン距離を求める

次のような文字列 A と文字列 B のレーベンシュタイン距離を求めるとします。

  • 文字列 A = “CARROT”
  • 文字列 B = “CAT”

文字列 A の文字数が i 文字、文字列 B の文字数が j 文字だとした場合の距離（最短変換数）を格納するための dp 配列を用意します。

dp[LenA + 1, LenB + 1]

下記の図は、この配列を表にしたものです。

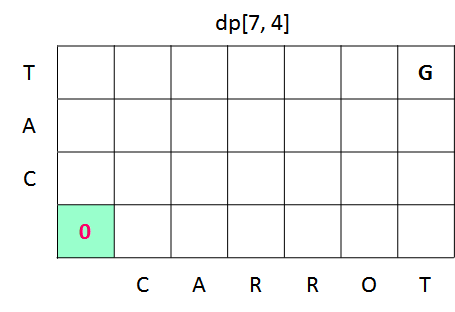
/p/xjw9ju7/img-001.png

セル内の数値は文字列を一致させるのに費やした変換手順数を表しており、dp[0, 0] は文字列 A も文字列 B も空文字だった場合の距離なので 0 です（空文字から空文字に変換するまでの手順数です）。 この表に左下から順番に手順数を埋めていき、最終的に右上の G が示している dp[7, 4] に文字列 A と文字列 B の距離が格納されます（“CAT” を “CARROT” に変換する手順数）。

ここでは、 文字列 B (“CAT”) を文字列 A (“CARROT”) に変換するためにかかる手順数 を求めていきます。 文字列 A を文字列 B に変換するためには逆の変換手順を行えばよいので、その手順数も同じになります。

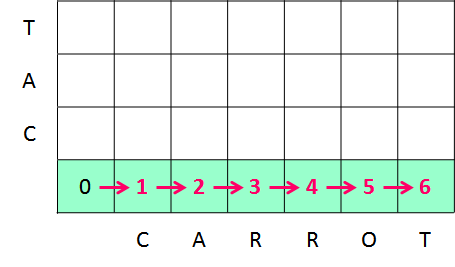
/p/xjw9ju7/img-002.png

dp[1, 0] は文字列 A の文字数が 1 文字（つまり “C” という文字列）、文字列 B の文字数が 0 文字（つまり空文字）だった場合に、文字列 B を文字列 A に変換するのにかかる手順数を示します。 この場合は、

空文字列 B に "C" という文字を追加して文字列 A に一致させる

という手順で一致させることができるので dp[1, 0] = 1 です。 dp[1, 0] の時点で構成される文字列は “C” です。

dp[2, 0] は空文字列 B を、文字列 A (“CA”) に一致させるための手順数を表します。 ここでのポイントは、dp[2, 0] を求めるときに、すでに計算済みの dp[1, 0] の値を利用して計算できるということです（動的計画法の考え方）。 dp[1, 0] には 1 文字目 (“C”) までを一致させるための手順数が格納されているので、あと 1 文字追加して 2 文字目まで (“CA”) を一致させるための手順数は次のような計算で求められます。

dp[2, 0] = dp[1, 0] + 1 = 2

同様に繰り返していくと、dp[6, 0] の時点で構成される変換後の文字列は、“CARROT” となり、変換手順数は 6 になります。 この過程で文字列 B（空文字列）が “CARROT” に変換されていく様子を示すと以下のようになります。

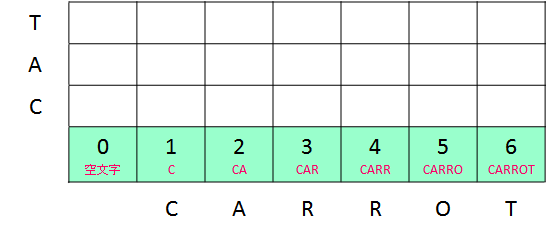
/p/xjw9ju7/img-003.png

簡単にいうと、文字を 1 文字ずつ追加する操作を 6 回行っているだけです。 ようするに、右方向への移動は、文字列 B への文字の追加を表しています。 上方向への移動は、逆に文字列 B から文字を削除して文字列 A に合わせていく操作を表します（もう一度繰り返しますが、ここでは、文字列 B (“CAT”) を文字列 A (“CARROT”) に変換する手順数を計算しています）。

下記は、文字列 B（“CAT”) から 3 文字の削除を行い、文字列 A（空文字）に一致させる操作を表現しています。 3 回の削除なので、dp[0, 3] = 3 となります。 変換後の文字列は空文字 "" です。

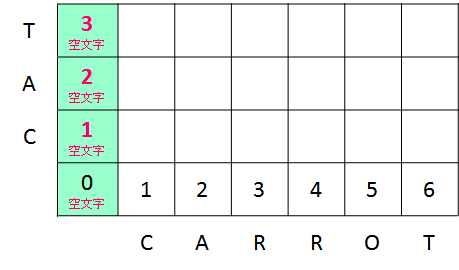
/p/xjw9ju7/img-004.png

次に dp[1, 1] を見てみます。 dp[0, 1] の "" の状態からの変化を考えると、“C” という文字を追加すれば文字列 A (“C”) に一致させることができます。

dp[1, 1] = dp[0, 1] + 1 = 2

上、右、と進む動きは、文字列 B から “C” を削除して、“C” を追加するという操作を示しています。 よく考えると同じ文字を削除して追加することは無駄な操作なのですが、あくまで、上方向への動きは文字列 B からの文字削除、右方向への動きは文字列 B への文字追加、というステップで変換していくことを表すので、この場合の合計手順数は 2 となります (dp[1,1] = 2)。

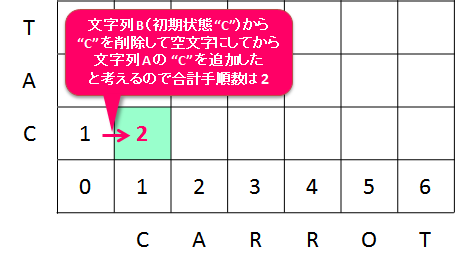
/p/xjw9ju7/img-005.png

dp[0, 1] の状態から進んでくる場合も同様に、dp[1, 1] = dp[0, 1] + 1 = 2 です。

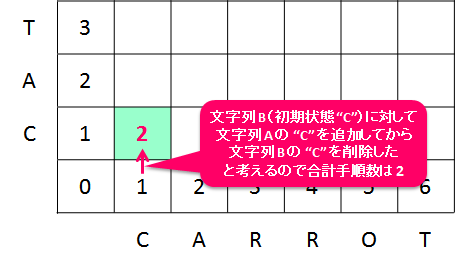
/p/xjw9ju7/img-006.png

この場合は、右、上と進んでくるので、文字列 B に対して “C” を追加してから、“C” を削除するという操作をしていることになります。 つまり、文字列 B に対して、以下のような変換操作をしています。

"C" => "CC" => "C"

無駄ですね。 そこで次に考慮するのが 斜め方向の移動 です。 斜め方向の移動は、

  • 変換を行わずに文字を一致させる（手順数＋0）
  • 文字列 B 側の文字を置換して文字列 A 側の文字に一致させる（手順数＋1）

のいずれかを表現します。

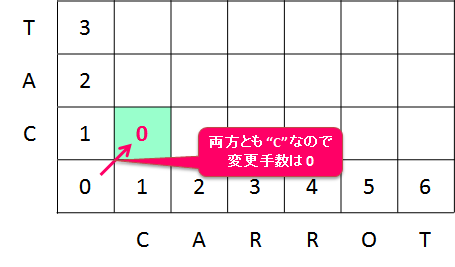
/p/xjw9ju7/img-007.png

今回のケースでは、文字列 A と B の 1 文字目はともに “C” という同じ文字なので、追加や削除の手順を踏まず（変換せず）に一文字目を一致させることができます。 なので、dp[1, 1] = dp[0, 0] + 0 = 0 という手順数で文字列を一致させることができます。 dp 配列にはそこに至るまでの最少手順数を格納するので、dp[1, 1] = 0 で確定です。 最初に計算した経路の手順数 2 は冗長なので採用しません。 手順数 0 でも同じ結果 “C” が得られるので、最少手順数である 0 を採用します。

文字列 A が “CARROT” ではなく “PARROT” であったらどうでしょう？ 下の図では、一致させようとしている文字が “C” と “P” で異なっているケースを示しています。

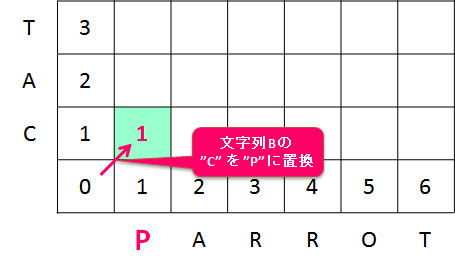
/p/xjw9ju7/img-008.png

レーベンシュタイン距離では、文字の置換も許可しているので、仮に、現在一致させようとしている文字（ここでは 1 文字目と 1 文字目）が異なっている場合、1 回の手順で変換して一致させることができます。 この例では、文字列 B の “C” という文字を、文字列 A の “P” という文字に合わせるように置換すればよいので、手順数は 1 となります (dp[1, 1] = dp[0, 0] + 1 = 1)。

重要な点は、dp[1, 1] という状態に至るまでにどのような変換経路をたどってきた場合でも、最終的に得られる結果（文字列 B から文字列 A への変換）は同じであるということです。 つまり、三種類の経路のうち、最小の手順数になるものを dp 配列に記憶していけばよいことになります。

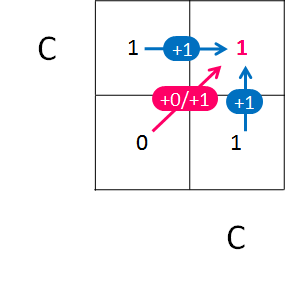
/p/xjw9ju7/img-009.png

以上のことを踏まえると、下記のような漸化式が導き出せます。

dp[i, j] = min(
    dp[i-1, j] + 1,
    dp[i, j-1] + 1,
    dp[i-1, j-1] + 0 or dp[i-1, j-1] + 1)

最後の or のところは、文字列 A の i 文字目、文字列 B の j 文字目が一致する場合に +0 となります。 異なる場合は、1 文字の置換操作を表すので +1 となります。

これを全セルに対して繰り返していくと、最終的に dp[LenA, LenB] に求める距離が格納されることになります。

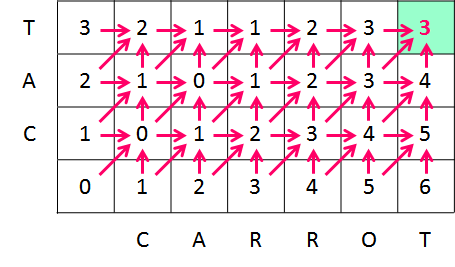
/p/xjw9ju7/img-010.png

右上の値は 3 になったので、最少手順で変換された場合の手順数は 3 回で、レーベンシュタイン距離は 3 ということになります。 変換の手順を示す経路は以下のようになります。

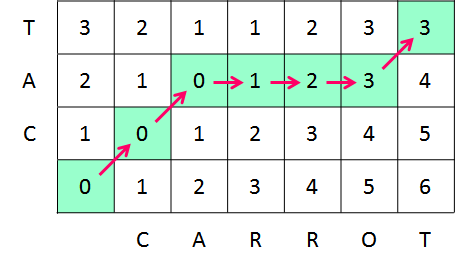
/p/xjw9ju7/img-011.png

具体的な変換手順はこうなります。

  1. “C” キープ（手順数 +0）
  2. “A” キープ（手順数 +0）
  3. “R” を挿入（手順数 +1）
  4. “R” を挿入（手順数 +1）
  5. “O” を挿入（手順数 +1）
  6. “T” キープ（手順数 +0）

この例では、最小の変換手順は 1 パターンしかありませんが、複数の変換パターンが存在することもあります。

Java による実装例

下記は二次元配列を使用した Java での実装例です。

Levenshtein.java
public class Levenshtein {
    /**
     * Calculate the Levenshtein distance between two strings.
     *
     * @param s1 the first string to be compared, not null
     * @param s2 the second string to be compared, not null
     * @return the distance between two strings
     * @see http://en.wikipedia.org/wiki/Levenshtein_distance
     */
    public static int getDistance(CharSequence s1, CharSequence s2) {
        int len1 = s1.length();
        int len2 = s2.length();
        int[][] dp = new int[len2 + 1][len1 + 1];
        // dp[0][0] = 0;
        for (int i = 1; i <= len1; ++i) {
            dp[0][i] = i;
        }
        for (int i = 1; i <= len2; ++i) {
            dp[i][0] = i;
        }
        for (int i = 1; i <= len2; ++i) {
            for (int j = 1; j <= len1; ++j) {
                if (s1.charAt(j - 1) == s2.charAt(i - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(dp[i - 1][j - 1] + 1,
                        Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
                }
            }
        }
        return dp[len2][len1];
    }

    public static void main(String[] args) {
        System.out.println(getDistance("", "")); // => 0
        System.out.println(getDistance("", "ABC")); // => 3
        System.out.println(getDistance("ABC", "")); // => 3
        System.out.println(getDistance("A", "ABC")); // => 2
        System.out.println(getDistance("ABC", "ABC")); // => 0
        System.out.println(getDistance("ABC", "XXXX")); // => 4
        System.out.println(getDistance("CXX", "XCCX")); // => 2
    }
}

二次元配列の更新は、1 行ずつしか行わないので、実は 2 つの一次元配列を使うだけで実装することができます。 下記は、一次元配列を使った実装例です。

public class Levenshtein {
    public static int getDistance(CharSequence s1, CharSequence s2) {
        int len1 = s1.length();
        int len2 = s2.length();
        int[] dp1 = new int[len1 + 1];
        int[] dp2 = new int[len1 + 1];
        for (int i = 0; i <= len1; ++i) {
            dp1[i] = i;
        }
        for (int i = 1; i <= len2; ++i) {
            dp2[0] = i;
            for (int j = 1; j <= len1; ++j) {
                if (s1.charAt(j - 1) == s2.charAt(i - 1)) {
                    dp2[j] = dp1[j - 1];
                } else {
                    dp2[j] = Math.min(dp1[j - 1] + 1,
                        Math.min(dp1[j] + 1, dp2[j - 1] + 1));
                }
            }
            // Swap buffers
            int[] temp = dp1;
            dp1 = dp2;
            dp2 = temp;
        }
        return dp1[len1];
    }
}

TypeScript による実装例

lib.ts
export class StringUtil {
  /**
   * 2つの文字列間のレーベンシュタイン距離を求めます。
   * 全く同じ文字列であれば、距離は 0 になります。
   */
  static calcLevenshtein(s1: string, s2: string): number {
    const len1 = s1.length;
    const len2 = s2.length;
    let dp1: number[] = []
    let dp2: number[] = []
    for (let i = 0; i <= len1; ++i) {
      dp1[i] = i;
    }
    for (let i = 1; i <= len2; ++i) {
        dp2[0] = i;
        for (let j = 1; j <= len1; ++j) {
            if (s1.charAt(j - 1) == s2.charAt(i - 1)) {
                dp2[j] = dp1[j - 1];
            } else {
                dp2[j] = Math.min(dp1[j - 1] + 1,
                    Math.min(dp1[j] + 1, dp2[j - 1] + 1));
            }
        }
        // Swap buffers
        [dp1, dp2] = [dp2, dp1];
    }
    return dp1[len1];
  }
}
使用例 (main.ts)
import { StringUtil } from './util';

console.log(StringUtil.calcLevenshtein("", "")); // => 0
console.log(StringUtil.calcLevenshtein("", "ABC")); // => 3
console.log(StringUtil.calcLevenshtein("ABC", "")); // => 3
console.log(StringUtil.calcLevenshtein("A", "ABC")); // => 2
console.log(StringUtil.calcLevenshtein("ABC", "ABC")); // => 0
console.log(StringUtil.calcLevenshtein("ABC", "XXXX")); // => 4
console.log(StringUtil.calcLevenshtein("CXX", "XCCX")); // => 2

関連記事

アルゴリズム 文字列
プログラム雑多メモ
へ戻る
まくろぐ
サイトマップ ｜ まくへのメッセージ